Refillable planet

Existing fertility interventions are (probably) well worth it

Humanity has a fertility problem. Birth rates are near or below replacement in all but the world’s poorest countries – and falling rapidly. Without a change in projected population trajectory (or AI timelines), humanity could have less than a century of current-level innovation left, forever.

What can we do? In the short term, countries will try to encourage immigration – see Japan’s recent liberalisation of immigration rules. But, fertility is falling everywhere. We might then try relying on the traditional driver of population growth over the past century, namely the lower mortality rates from economic growth and medical advancements. However, the gains from this approach have been exhausted. People rarely die before reaching the age at which they would have stopped having children.¹

So, we’re left with trying to encourage more births, or removing barriers that exist currently. More people are good. Not only are they capable of leading happy lives (a philosophical position), but they have ideas, and innovate. However, it is not immediately clear if we, like good economists, should subsidise this positive externality. This is because, bar some sophisticated (and politically difficult) targeting, we’ll have to subsidise all births, including those that would’ve happened anyway. 

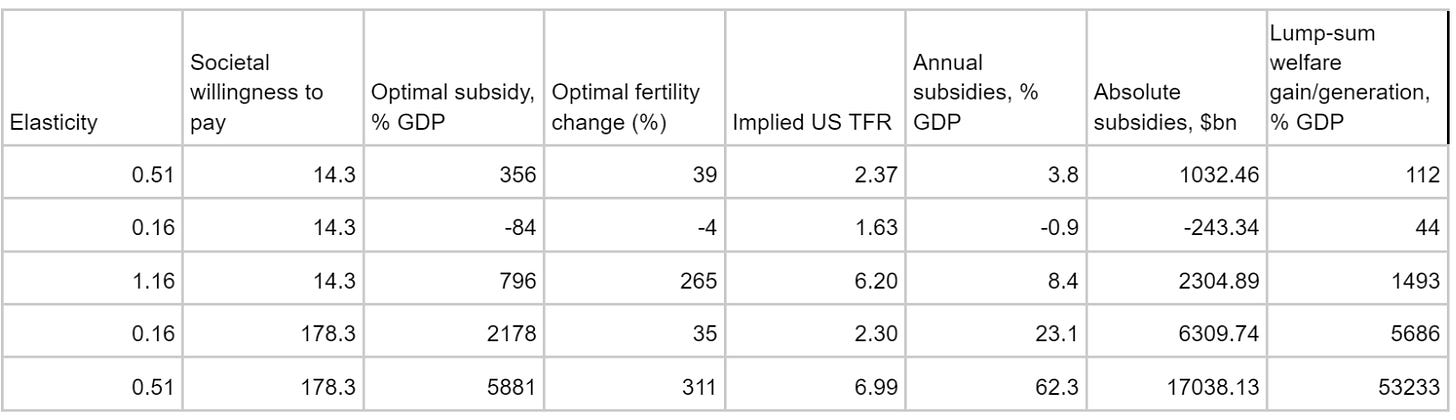
In this post, we show that under the median estimated elasticity the socially optimal fertility rate is 2.4 in the US, well above today’s 1.7, given that the US should place a value of 14.28x GDP/capita per additional birth ($1.17mn per birth). Furthermore, to achieve this, the US should be willing to spend the equivalent of 3.8% of its GDP ($290K per birth) on fertility subsidies. For context, the existing child tax credit is worth $2000/year, or $26K present value. We’d like to stress that these figures are highly uncertain, because of both the varying welfare gain from more births, and also varying estimates of how effective subsidising births are. Even still, in the main case, the US government should seriously consider greatly increasing its child tax credits, and explore more creative and ambitious solutions to address this looming demographic crisis. 

How much should we be willing to pay for an additional birth? 

There are probably four reasons why you should care about increasing fertility rates: public goods (the fixed cost for public goods are spread across more productive people), externalities from research (more people, more ideas!), life cycle effects (the young can help the old) and altruism (we care about the happiness of future generations).

Firstly, more people, more ideas. Ideas have been the driver of economic growth, and people are the driver of ideas. And ideas are ‘non-rival’ - if we invent a better way to grow wheat, it doesn’t matter whether the technique is used by 100 people, or a million. To figure out how valuable these new people and their ideas are, we work out the value of the worlds where they did and did not exist. There are a couple of considerations we need to make these calculations. However, the quality and quantity of ideas (as measured by their economic contribution) does not increase in direct proportion to the number of people. They suffer from diminishing returns which means we should multiply each additional person’s output by 0.75. Because we’re only concerned with the US, using the contributions of scientists to published research as a proxy for total contribution to scientific output, the US accounts for only 26% of global science output.²  We must also remember that the new births are children, and so we should apply a discount factor of 0.82.³ The Economist, arguing against the subsidies we model, noted that only 8% of children of parents without college education will get a college degree, compared to 62% of all parents. However, even if we fully account for this, this still yields a $1.03m (around 12.67xGDP/capita) willingness to pay for any given birth from just their research contributions.⁴

Now we also should add the additional benefit from spreading the fixed cost for public goods, eg. on defence or public debt, across more people. Such public goods are “non-rival”, which means that they don’t get worse for existing users if more people use them. As a result, if we increase births, we increase the number of people who can pay for them, and hence reduce costs for existing users. For the US, we model just the military and public debt, subtracting climate change. The US devotes 3.4% GDP to the military and has debt worth 122% of GDP. And, how about increasing birth’s effects on climate change? Well, though the aggregate costs of climate change increase faster than the population, it’s not by much, with an elasticity of 1.18.⁵ When we consider this with a 3.5% discount rate the present value decarbonisation expenses are equivalent to 23% GDP for purposes here, overall resulting in the 1.96xGDP gains from the other public good effects, which we also discount by 0.82. 

Next, higher fertility means younger people. In the medium term, this results in higher taxes per capita. Unfortunately, we don’t have good figures of the marginal government spending over a lifetime by age. Both caring for the elderly and educating children are expensive - so we don’t know what the net effect will be, because the elderly are much more expensive per person, but their costs are also far in the future. We’ll leave this out of our calculations for now. 

Finally, we’ll briefly consider the “full altruism” case, ie. one where we also value the raw happiness enjoyed by these new people. A life is worth much more than a total lifetime income.⁶ We get this from considering the statistical value of life, currently $13m, which is much higher than expected lifetime income. This yields a 164x GDP in the US. We don’t include this number for our baseline estimates – whether or not to do so philosophically controversial - but do present results if this utilised.

Model

Now that we have society’s “willingness to pay” for an additional birth, we need to estimate how responsive fertility is to a subsidy. 

Suppose that fertility, n, has a constant elasticity to the private value of having a child, so takes the form:

\(n = n_0 (1+\frac{s}{v})^{\mu}\)

Given that the policymaker places social externality k (calculated above) and private value v on each birth, they will try to maximise:

\((k+v-s)(1+\frac{s}{v})^{\mu}\)

This solves to

\(s^{*} = \frac{\mu k - v(1-\mu)}{\mu + 1}\)

Which means that, with the optimal subsidy, fertility will increase to:

\(n^{*} = n_0 (\frac{\mu}{\mu+1})^{\mu} (2+\frac{k}{v})^{\mu}\)

We can therefore see that the condition for this subsidy being greater than zero is that the elasticity needs to be greater than the private value over the social value, or: 

\(\mu > \frac{v}{k+v}\)

Quickly estimating the rest of the parameters:

• v is the perceived value of raising a child. On the margin, this will equal the perceived cost of raising a child. In the US, this was $233,000 in 2017, or 3.88. 

• mu is the elasticity. This literature review estimates that the elasticity of fertility to a payment equivalent to 1% of income is between 0.04-0.3. We then need to multiply this by 3.88, because we’re interested in the elasticity to the private valuation v, getting 0.15 to 1.16, with median estimate 0.51.

Results and discussion

We find that, for any intervention, the elasticity for fertility needs to exceed 0.27 – if you only care about the research and public goods externalities. This means that most existing interventions would be well worth the money if implemented in the US.⁷⁸ While the recommended payments are substantial, if US borrowing isn’t too large a share of overall capital markets then the large size of these payments won’t pose a problem.⁹

We should also note that our estimates are a static, not dynamic model, meaning that our estimates are conservative. If we consider the world where, as a result of this policy, the population itself increases – and this causes many of the effects we model (both positive and negative) to change as well. Because, under our estimates, the positive effects likely increase by much more than the negative, a dynamic model of this policy means that we should be even more willing to pay for more births.¹⁰

The other effect that we do not include is the welfare gains from the non-marginal parent who now gets a free subsidy for children they would’ve had anyway, and are now strictly better off. We treat their welfare gain from this as zero, and so overestimate the costs.

One billion Americans

We conclude that the US government should be willing to pay up to $290,000, overall, to each parent who gives birth. This is a result of our model that shows that any new child born, that wouldn’t otherwise have been born without the subsidy, has a $1.17mn value to the US. In practice, suggestions for additional child tax credits from across the aisle should be implemented, and perhaps even greatly increased. 

Because there is a huge range of elasticity estimates in the literature, there is only so much confidence we can ascribe to any policy implications. Existing interventions aren’t well studied. And we’re interested in the best interventions, not the average ones. Society should invest more resources in studying fertility interventions worldwide, and coming up with new ones: subsidising fertility treatment, reforming child care regulation, changing cultural norms. 

For this post, though, in many senses, we’ve modelled the worst case. That these subsidies are non-targeted, while in practice, we can do much better. That more young people won’t improve the demographic structure of the economy, while in practice, it will. That society doesn’t account for the happiness of the new children themselves, while in practice, we do. 

Humanity has a fertility problem. But it’s a solvable one.

1. Unintuitively, increases in the growth rate of life expectancy only have level effects on population, as long as life expectancy growth remains below 1 year/year. This is because increases in life expectancy don’t result in additional births from individuals of childbearing age surviving when they would instead have died, but instead lower the mortality of individuals beyond it.

2.  We’ll assume that research output flows perfectly across borders; due to patents often being recognised internationally this will lead to a slight underestimate of the gains.

3. Children aren’t immediately productive, but have more years of working life remaining than the median American, so it is prima facie unclear whether they will be more or less productive. Under a 3.5% discount rate, the net effect is to render their present value 82% of average at birth. 

4. This is likely a large underestimate of the research potential of the additional births induced; some individuals with higher educational levels will respond to the incentives, while comparative advantage will ensure that even if the assumptions about who will be incentivised were correct research output would still rise.

5. Global per capita costs of climate change would rise from $471 to $481 in the event of a rise in the global population from 8.7bn to 9.7bn.

6. Because the happiness that a person diminishes from increased income, so you value your “previous” consumption more than you paid for it in your marginal consumption.

7. It doesn’t necessarily follow from this that the interventions were worthwhile in the countries in which they were conducted: as the benefits in this model are almost entirely driven by research externalities, and a country’s incentive to do this scales with size, fertility interventions in very small countries may not have paid off.

8.  In the long-run, the standard model for fertility, the Barro-Becker model, would predict that when the cost of children falls, people will have more children. However, they’ll have so many more children, they’ll give each less of an inheritance, and this’ll result in their incomes decreasing so much that the resulting reduction of children that they’ll in turn have will have decreased have so much that overall they would’ve had as many children as if the decline had never occurred. In short, the subsidy would only have boosted births one time, and births would fall by as much if it was withdrawn.

The empirical fit of the model without extensive modifications is dubious though - it predicts very large dependence of fertility on interest rates, and struggles to yield a declining crude birth rate in response to falls in infant mortality. 

9. If the US accounted for a very large share of global borrowing, then if payments became large as a fraction of GDP then diminishing marginal utility of income would reduce willingness to pay, as although additional children would continue to bring large benefits the current consumption traded off against it would become increasingly costly. However, future productivity gains can be borrowed against to avoid a reduction in living standards today. 

10. Research externalities rise quickly with population; climate change rises slowly and public goods benefits fall slowly with it, but the population could double from its present level and the public goods - climate term would remain positive, while the research term would double. Importantly, under a higher population reaching above replacement fertility could be optimal while it previously was not - policymakers would be willing to spend on short-run-negative subsidies as with the higher population new possibilities would be opened.